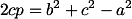PengantarPada pembahasan mengenai pokok bahasan kinematika (gerak lurus dan gerak bengkok, kita telah menyinggung mengenai Gravitasi. Pada kesempatan ini, kita akan mempelajari Gravitasi secara lebih mendalam.
Mengapa buah mangga yang lezat dan bergizi yang terlepas dari tangkainya selalu jatuh ke permukaan bumi ? ayo dijawab…
Selain mengembangkan tiga hukum tentang Gerak (Hukum I Newton, Hukum II Newton dan Hukum III Newton), eyang Newton juga menyelidiki gerakan planet-planet dan bulan. Ia selalu bertanya mengapa bulan selalu berada dalam orbitnya yang hampir berupa lingkaran ketika mengitari bumi. Selain itu, ia juga selalu mempersoalkan mengapa benda-benda selalu jatuh menuju permukaan bumi. Wililiam Stukeley, teman eyang Newton ketika masih muda, menulis bahwa ketika mereka sedang duduk minum teh di bawah pohoh apel, eyang Newton yang waktu itu masih muda dan cakep, melihat sebuah apel jatuh dari pohonnya. Dikatakan bahwa eyang Newton mendapat ilham dari jatuhnya buah apel. Menurutnya, jika gravitasi bekerja di puncak pohon apel, bahkan di puncak gunung, maka mungkin saja gravitasi bekerja sampai ke bulan. Dengan penalaran bahwa gravitasi bumi yang menahan bulan pada orbitnya, eyang Newton mengembangkan teori gravitasi yang sekarang diwariskan kepada kita.
Perlu diketahui bahwa persoalan yang dipikirkan eyang Newton ini telah ada sejak zaman yunani kuno. Ada dua persoalan dasar yang telah diselidiki oleh orang yunani, jauh sebelum eyang Newton lahir. Persoalan yang selalu dipertanyakan adalah mengapa benda-benda selalu jatuh ke permukaan bumi dan bagaimana gerakan planet-planet, termasuk matahari dan bulan (matahari dan bulan pada waktu itu digolongkan menjadi planet-planet). Orang-orang Yunani pada waktu itu melihat kedua persoalan di atas (benda yang jatuh dan gerakan planet) sebagai dua hal yang berbeda. Demikian hal itu berlanjut hingga zaman eyang Newton. Jadi apa yang dihasilkan oleh eyang dibangun di atas hasil karya orang-orang sebelum dirinya. Yang membedakan eyang Newton dan orang-orang sebelumnya adalah bahwa eyang memandang kedua persoalan dasar di atas (gerak jatuh benda dan gerakan planet) disebabkan oleh satu hal saja dan pasti mematuhi hukum yang sama. Pada abad ke-17, eyang menemukan bahwa ada interaksi yang sama yang menjadi penyebab jatuhnya buah apel dari pohon dan membuat planet tetap berada pada orbitnya ketika mengelilingi matahari. Demikian juga bulan, satu-satunya satelit alam kesayangan bumi tetap berada pada orbitnya.
Mari kita belajar hukum dasar cetusan eyang Newton yang kini diwariskan kepada kita. Hukum dasar inilah yang menentukan interaksi gravitasi. Ingat bahwa hukum ini bersifat universal alias umum; gravitasi bekerja dengan cara yang sama, baik antara diri kita dengan bumi, antara bumi dengan buah mangga yang lezat ketika jatuh, antara bumi dengan pesawat yang jatuh
, antara planet dengan satelit dan antara matahari dengan planet-planetnya dalam sistem tatasurya.
Oya lupa….
Tahukah anda, bahkan gagasan eyang Newton mengenai gravitasi pada mulanya
dibantai habisan-habisan oleh banyak ilmuwan yang bertentangan dengan gagasannya ? Pada waktu itu, banyak ilmuwan yang mungkin saking kebingungan sulit menerima gagasan eyang Newton mengenai gaya gravitasi. Gaya gravitasi termasuk gaya tak sentuh, di mana bekerja antara dua benda yang berjauhan alias tidak ada kontak antara benda-benda tersebut. Gaya-gaya yang umumnya dikenal adalah gaya-gaya yang bekerja karena adanya kontak; gerobak sampah bergerak karena kita memberikan gaya dorong, bola bergerak karena ditendang,
sedangkan gravitasi,
bisa bekerja tanpa sentuhan ? aneh… eyang Newton mengatakan kepada mereka bahwa ketika apel jatuh, bumi memberikan gaya kepadanya sehingga apel tersebut jatuh, demikian juga bumi mempertahankan bulan tetap pada orbitnya dengan gaya gravitasi, meskipun tidak ada kontak dan letak bumi dan bulan berjauhan. Akhirnya, perlahan-lahan sambil bersungut-sungut mereka mulai merestui dan mendukung dengan penuh semangat Hukum Gravitasi yang dicetuskan oleh Eyang Newton
HUKUM GRAVITASI NEWTON
Sebelum mencetuskan Hukum Gravitasi Universal, eyang Newton telah melakukan perhitungan untuk menentukan besar gaya gravitasi yang diberikan bumi pada bulan sebagaimana besar gaya gravitasi bumi yang bekerja pada benda-benda di permukaan bumi. Sebagaimana yang kita ketahui, besar percepatan gravitasi di bumi adalah 9,8 m/s2. Jika gaya gravitasi bumi mempercepat benda di bumi dengan percepatan 9,8 m/s2, berapakah percepatan di bulan ? karena bulan bergerak melingkar beraturan (gerakan melingkar bulan hampir beraturan), maka percepatan sentripetal bulan dihitung menggunakan rumus percepatan sentripetal Gerak melingkar beraturan.
Diketahui orbit bulan yang hampir bulat mempunyai jari-jari sekitar 384.000 km dan periode (waktu yang dibutuhkan untuk melakukan satu putaran) adalah 27,3 hari. Dengan demikian, percepatan bulan terhadap bumi adalah
Jadi percepatan gravitasi bulan terhadap bumi 3600 kali lebih kecil dibandingkan dengan percepatan gravitasi bumi terhadap benda-benda di permukaan bumi. Bulan berjarak 384.000 km dari bumi. Jarak bulan dengan bumi ini sama dengan 60 kali jari-jari bumi (jari-jari bumi = 6380 km). Jika jarak bulan dari bumi (60 kali jari-jari bumi) dikuadratkan, maka hasilnya sama dengan 3600 (60 x 60 = 602 = 3600). Angka 3600 yang diperoleh dengan mengkuadratkan 60 hasilnya sama dengan Percepatan bulan terhadap bumi, sebagaimana hasil yang diperoleh melalui perhitungan.
Berdasarkan perhitungan ini, eyang newton menyimpulkan bahwa besar gaya gravitasi yang diberikan oleh bumi pada setiap benda semakin berkurang terhadap kuadrat jaraknya (r) dari pusat bumi. Secara matematis dapat ditulis sebagai berikut :
Selain faktor jarak, Eyang Newton juga menyadari bahwa gaya gravitasi juga bergantung pada massa benda. Pada Hukum III Newton kita belajar bahwajika ada gaya aksi maka ada gaya reaksi. Ketika bumi memberikan gaya aksi berupa gaya gravitasi kepada benda lain, maka benda tersebut memberikan gaya reaksi yang sama besar tetapi berlawanan arah terhadap bumi. Karena besarnya gaya aksi dan reaksi sama, maka besar gaya gravitasi juga harus sebanding dengan massa dua benda yang berinteraksi. Berdasarkan penalaran ini, eyang Newton menyatakan hubungan antara massa dan gaya gravitasi. Secara matematis ditulis sbb :
MB adalah massa bumi, Mb adalah massa benda lain dan r adalah jarak antara pusat bumi dan pusat benda lain.
Setelah membuat penalaran mengenai hubungan antara besar gaya gravitasi dengan massa dan jarak, eyang Newton membuat penalaran baru berkaitan dengan gerakan planet yang selalu berada pada orbitnya ketika mengitari matahari. Eyang menyatakan bahwa jika planet-planet selalu berada pada orbitnya, maka pasti ada gaya gravitasi yang bekerja antara matahari dan planet serta gaya gravitasi antara planet, sehingga benda langit tersebut tetap berada pada orbitnya masing-masing. Luar biasa pemikiran eyang Newton ini. Tidak puas dengan penalarannya di atas, ia menyatakan bahwa jika gaya gravitasi bekerja antara bumi dan benda-benda di permukaan bumi, serta antara matahari dan planet-planet maka mengapa gaya gravitasi tidak bekerja pada semua benda ?
Akhirnya, setelah bertele-tele dan terseok-seok, kita tiba pada inti pembahasan panjang lebar ini. Eyang Newton pun mencetuskan Hukum Gravitasi Universal dan mengumumkannya pada tahun 1687, hukum yang sangat terkenal dan berlaku baik di indonesia, amerika atau afrika bahkan di seluruh penjuru alam semesta. Hukum gravitasi Universal itu berbunyi demikian :
Semua benda di alam semesta menarik semua benda lain dengan gaya sebanding dengan hasil kali massa benda-benda tersebut dan berbanding terbalik dengan kuadrat jarak antara benda-benda tersebut.
Secara matematis, besar gaya gravitasi antara partikel dapat ditulis sbb :
Fg adalah besar gaya gravitasi pada salah satu partikel, m1 dan m2 adalah massa kedua partikel, r adalah jarak antara kedua partikel.
G adalah konstanta universal yang diperoleh dari hasil pengukuran secara eksperimen. 100 tahun setelah eyang Newton mencetuskan hukum Gravitasi Universal, pada tahun 1978, Henry Cavendish berhasil mengukur gaya yang sangat kecil antara dua benda, mirip seperti dua bola. Melalui pengukuran tersebut, Henry membuktikan dengan sangat tepat persamaan Hukum Gravitasi Universal di atas. Perbaikan penting dibuat oleh Poyting dan Boys pada abad kesembilan belas. Nilai G yang diakui sekarang = 6,67 x 10-11Nm2/kg2
Contoh soal 1 :
Seorang guru fisika sedang duduk di depan kelas dan seorang murid sedang duduk di bagian belakang ruangan kelas. Massa guru tersebut adalah 60 kg dan massa siswa 70 kg (siswa gendut). Jika pusat mereka (yang dimakudkan di sini bukan pusat yang terletak di depan perut manusia) berjarak 10 meter, berapa besar gaya gravitasi yang diberikan oleh guru dan murid satu sama lain ?
Panduan jawaban :
Gampang, tinggal dimasukkan aja nilai-nilai telah diketahui ke dalam persamaan Hukum Newton tentang Gravitasi
Ya, gayanya sangat kecil…
Contoh soal 2 :
Diketahui massa bulan 7,35 x 1022 kg, massa bumi 5,98 x 1024 kg dan massa matahari adalah 1,99 x 1030 kg. Hitunglah gaya total di bulan yang disebabkan oleh gaya gravitasi bumi dan matahari. Anggap saja posisi bulan, bumi dan matahari membentuk segitiga siku-siku. Oya, jarak bumi-bulan 3,84 x 108 m dan jarak matahari-bulan 1,50 x 108 km (1,50 x 1011 m).
Keterangan Gambar :
b = bulan, B = bumi dan M = matahari
Panduan jawaban :
Gaya total yang bekerja pada bulan akibat gravitasi matahari dan bumi kita hitung menggunakan vektor. Sebelumnya, terlebih dahulu kita hitung besar gaya gravitasi antara bumi-bulan dan matahari-bulan.
Besar gaya gravitasi antara bumi-bulan :
Besar gaya gravitasi antara matahari-bulan.
Besar gaya total yang dialami bulan dapat dihitung sebagai berikut :
Gaya total yang dimaksud di sini tidak sama dengan gaya total pada Hukum II Newton. Hukum gravitasi berbeda dengan Hukum II Newton. Hukum Gravitasi menjelaskan gaya gravitasi dan besarnya yang selalu berbeda tergantung dari jarak dan massa benda yang terlibat. Hukum II Newton menghubungkan gaya total yang bekerja pada sebuah benda dengan massa dan percepatan benda tersebut. Dipahami ya perbedaannya….
Kuat Medan Gravitasi dan Percepatan Gravitasi
Pada pembahasan mengenai Hukum Newton tentang Gravitasi, kita telah meninjau gaya gravitasi sebagai interaksi gaya antara dua atau lebih partikel bermassa. Partikel-partikel tersebut dapat saling berinteraksi walaupun tidak bersentuhan. Pandangan lain mengenai gravitasi adalah konsep medan, di mana sebuah benda bermassa mengubah ruang di sekitarnya dan menimbulkan medan gravitasi. Medan ini bekerja pada semua partikel bermassa yang berada di dalam medan tersebut dengan menimbulkan gaya tarik gravitasi. Jika sebuah benda berada di dekat bumi, maka terdapat sebuah gaya yang dikerjakan pada benda tersebut. Gaya ini mempunyai besar dan arah di setiap titik pada ruang di sekitar bumi. Arahnya menuju pusat bumi dan besarnya adalah mg.
Jadi jika sebuah benda terletak di setiap titik di dekat bumi, maka pada benda tersebut bekerja sebuah vektor g yang sama dengan percepatan yang akan dialami apabila benda itu dilepaskan. Vektor g tersebut dinamakan kekuatan medan gravitasi. Secara matematis, besar g dinyatakan sebagai berikut :
Berdasarkan persamaan di atas, kita dapat mengatakan bahwa kekuatan medan gravitasi di setiap titik merupakan gaya gravitasi yang bekerja pada setiap satuan massa di titik tersebut.
Gravitasi di Sekitar Permukaan Bumi
Pada awal tulisan ini, kita telah mempelajari Hukum gravitasi Newton dan menurunkan persamaan gravitasi Universal. Sekarang kita mencoba menerapkannya pada gaya gravitasi antara bumi dan benda-benda yang terletak di permukaannya. Kita tulis kembali persamaan gravitasi universal untuk membantu kita dalam menganalisis :
Untuk persoalan gravitasi yang bekerja antara bumi dan benda-benda yang terletak di permukaan bumi, m1 pada persamaan di atas adalah massa bumi (mB), m2 adalah massa benda (m), dan r adalah jarak benda dari permukaan bumi, yang merupakan jari-jari bumi (rB). Gaya gravitasi yang bekerja pada bumi merupakan berat benda, mg. Dengan demikian, persamaan di atas kita ubah menjadi :
Berdasarkan persamaan ini, dapat diketahui bahwa percepatan gravitasi pada permukaan bumi alias g ditentukan oleh massa bumi (mB) dan jari-jari bumi (rB)
G dan g merupkan dua hal yang berbeda. g adalah percepatan gravitasi, sedangkan G adalah konstanta universal yang diperoleh dari hasil pengukuran. Setelah G ditemukan, manusia baru bisa mengetahui massa bumi lewat perhitungan menggunakan persamaan ini. Hal ini bisa dilakukan karena telah diketahui konstanta universal, percepatan gravitasi dan jari-jari bumi.
Ini adalah persamaan percepatan gravitasi efektiv. Jika ditanyakan percepatan gravitasi pada ketinggian tertentu di dekat permukaan bumi, maka kita dapat menggunakan persamaan ini. Jika kita menghitung berat benda yang terletak di permukaan bumi, kita menggunakan mg.
