Kevin 08 07 28 BLogspot: Dalil Steward

Wew... Ternyata dalil ini sungguh sangat berguna dalam menyelesaikan berbagai masalah dalam garis-garis segitiga. Contohnya pada soal berikut:

Contoh Soal:
Jika AB = 10 cm, CB = 12 cm, AC = 6 cm, dan DB = 7 cm, maka berapakah panjang CD?
(jangan dijawab di sini doeloe yach)... ^^

Sebelum mengenal dalil Steward, alangkah baiknya kalau kita mengenal apa itu proyeksi.

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Mengenal Proyeksi
Hmm. Perhatikan gambar berikut.

Jika ruas garis AB diproyeksikan ke garis l, maka hasilnya adalah sebagai berikut.

Dari gambar di atas, AA' tegak lurus terhadap garis l dan BB' tegak lurus terhadap garis l. A'B' adalah proyeksi AB pada l.

Sedangkan, apabila ruas garis l diproyeksikan terhadap AB, maka hasilnya adalah sebagai berikut.

Pada gambar di atas, ruas garis yang berwarna merah adalah proyeksi ruas garis l terhadap AB.
Tentunya, dari kedua contoh di atas, kalian sudah tahu istilah proyeksi bukan.? Jadi, proyeksi itu seperti memetakan suatu daerah secara tegak lurus terhadap daerah lainnya. Begitu loh... ^^

Contoh soal 1:
Tentukan proyeksi dari:

a. AB pada BC
b. BC pada AC
c. AB pada AC
d. AC pada BC
e. BC pada AB
f. AC pada AB

Jawab: a. BD; b. CE; c. AE; d. CD; e. BF; f. AF.

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Rumus Proyeksi Pada Segitiga Lancip

Perhatikan gambar di samping!
$\triangle$ ABC adalah segitiga lancip.
CF $\perp$ AB (CF=garis tinggi)
AF = p(proyeksi AC pada AB), maka BF = c-p

________

Perhatikan $\triangle$ ACF
$t^2=b^2-p^2$

Perhatikan $\triangle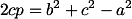$ BCF
$t^2=a^2-BF^2$
$t^2=a^2-(c-p)^2$

__________

Sehingga:
$b^2-p^2=a^2-(c-p)^2$
$b^2-p^2=a^2-(c^2-2cp+p^2)$
$\usepackage{cancel} b^2-\cancel{p^2}=a^2-c^2+2cp-\cancel{p^2}$

$p=\frac{b^2+c^2-a^2}{2c}$

==>rumus proyeksi AC pada AB
___pada segitiga lancip

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Rumus Proyeksi Pada segitiga Tumpul

Perhatikan gambar di samping!
$\triangle$ ABC adalah segitiga tumpul.
CF $\perp$ AB (CF=garis tinggi)
AF = p (proyeksi AC pada AB).

________

Perhatikan $\triangle$ ACF
$t^2=b^2-p^2$

Perhatikan $\triangle$ BFB
$t^2=a^2-BF^2$
$t^2=a^2-(c+p)^2$

__________

Sehingga:
$b^2-p^2=a^2-(c+p)^2$
$b^2-p^2=a^2-(c^2+2cp+p^2)$
$\usepackage{cancel} b^2-\cancel{p^2}=a^2-c^2-2cp-\cancel{p^2}$
$-2cp=b^2+c^2-a^2$

$p=-\left(\frac{b^2+c^2-a^2}{2c}\right)$

==>rumus proyeksi AC pada AB
___pada segitiga tumpul

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Dalil Stewart

Nah, sekarang baru kita akan membahas dalil Stewart. Kenapa kita harus terlebih dahulu tahu tentang proyeksi?? Karena dalil Stewart menggunakan dasar rumus tersebut... Let's check it out..!!! XDXDXD

ABC adalah segitiga sembarang. D adalah sembarang titik pada sisi AB. AD= $c_1$ dan DB = $c_2$ .
Jika a, b, c, $c_1$ , dan $c_2$ diketahui, maka panjang CD (l) dapat dihitung sebagai berikut.

Perhatikan $\triangle$ ACD,
$p=\frac{c_1^2+\overline{CD}^2-b^2}{2c_1}$
Perhatikan $\triangle$ BCD,
$p=-\left(\frac{c_2^2+\overline{CD}^2-a^2}{2c_2}\right)$

Gabungkan keduanya, maka:

$\frac{c_1^2+\overline{CD}^2-b^2}{2c_1}=-\left(\frac{c_2^2+\overline{CD}^2-a^2}{2c_2}\right)$

Kali silang, lalu bagi dengan 2, maka:

$c_2c_1^2+c_2\overline{CD}^2-c_2b^2=-c_1c_2^2-c_1\overline{CD}^2+c_1a^2$

$(c_1+c_2)\overline{CD}^2=c_1a^2+c_2b^2-c_1c_2^2-c_1^2c_2$

$\overline{CD}^2.(c_1+c_2)=c_1a^2+c_2b^2-c_1c_2(c_1+c_2)$

Ingat bahwa $c_1+c_2=c$ , maka:

$\overline{CD}^2.c=c_1a^2+c_2b^2-c_1c_2c$

Rumus di atas itulah yang sering dikenal debagai dalil Stewart.

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=
Contoh Soal 2:

Jika AB = 10 cm, CB = 12 cm, AC = 6 cm, dan DB = 7 cm, maka berapakah panjang CD?

Jawab:
$AB\overline{CD}^2=AD.BC^2+BD.AC^2-AD.BD.AB$
$10.\overline{CD}^2=3.12^2+7.6^2-3.7.10$
$10.\overline{CD}^2=474$
$\overline{CD}=\sqrt{47,4}$
$\overline{CD}=\text{6,88}$ _________==> menggunakan kalkulator.

=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=

Selanjutnya, dalil Stewart sangat terpakai terutama untuk menghitung panjang garis-garis istimewa pada segitiga. Silakan cek bagian "Garis-Garis Istimewa pada Segitiga", untuk melihat sambungan/lanjutan materi ini. ^^

Laman

Minggu, 19 Desember 2010

Dalil Steward

Tidak ada komentar:

Posting Komentar

Menurut anda,penampilan Blog ini bagaimana?